New personal record today.

[Halo]

(quote)  Oh, it's not that there's no visitors, it's just that it's a permanent move and you wouldn't like the neighbors. (unquote)



Excellent perspective, Saxman!

(Incidentally, do you play alto, tenor, or bari?)

[B@tfinkV]

i think youre totaly wrong chairboy. your original tartly correction of jebus's fun hypothesis got under my skin. you want to crush his and maybe even my fun because you think you truly know what happens at the center of gravity just like any scientist can have a clue for sure....yeah.

my version makes perfect sense, and you still seem to think that if an object is at the center of the earths gravitational field without the physical matter of the earth to get in the way that you could describe gravity as 'pulling' you anywhere.

my comments were not intentionaly snarky i was just light spirited same as jebus when he suggested something that we can never proove for real anyhow. i just saw you as jumping in to crush the idea before we had any fun with it. geuss the fact that you have said some pretty funny things in anger directed at some people im friends with here maybe puts me in a hostile mood with you so i appologise for that.

but youre still wrong and whoever backs you up is wrong for your original wording correction, i stand by:

if no there is no seperation between the very center source of a force and an object then 'pulling' is not a word that can be applied unless one or both forces or objects are in another plane of motion independant from each other.

[rpm]

Originally posted by Curval
That would FREAK me out being so far down.  Honestly.  The thought of all that rock and dirt above me...nope.  Not into it.

Holy CRAP Rogwar!

I'm on the verge of a panic attack just thinking about being that deep!:eek: I hope you are paid very, very well for your services.

[shamroc]

Originally posted by rpm
Holy CRAP Rogwar!

I'm on the verge of a panic attack just thinking about being that deep!:eek: I hope you are paid very, very well for your services.

Serious question - has anyone ever sent anything down there ?

I mean, how can we really know for sure what's down there until we actually send something down there....

Assuming we sent down a highly resilient web cam at the end of a proverbial very long stick... would we be greeted with zero gravity, or the maniacal  smiling face of the dark lord himself ?

Shamroc

[clerick]

Ok, maybe a little multimedia presentation will sort this out.

Force due to gravity is an inversely affected by the square of the distance between the center of mass.



Now you could view the earth as a number of really really small but equal masses; think really really small pieces of rock and each is a separate object that just happens to be placed really really close to other really really small rocks.



But, if you assume the Earth is a sphere of constant mass (which it isn't), you can combine all those smaller masses into one big mass and the math will work out the same. Plug in some simple values and you will see that this is true.



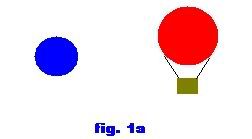
However, things get a bit tricky once you place one object within the other, because now you have to start looking at it as a bunch of smaller masses again.  This is because the entire mass of the one object is no longer "pulling: the second object in the same direction.  Simply illustrated, it would be like placing one object equidistant from two identical masses.



Now, if we extrapolate this to the idea of an object at the center of he Earth, and treat the Earth no as one large mass, but as an infinite number of smaller, but equal, masses you could visualize it like this. (not to scale)



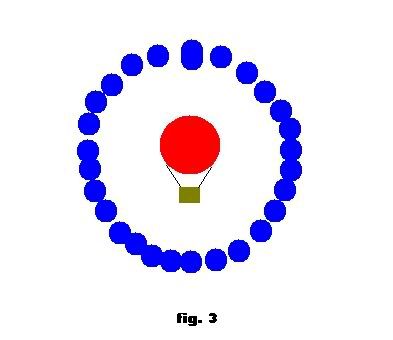
Each one of those masses wants to pull the poor balloon towards it, but since they are all theoretically the same mass, and the balloon is hypothetically in the exact center of the smaller masses, the balloon will stay where it is.

I have oversimplified things and ignored a number of other factors...

The Earth is not a true sphere

The Earth's density and mass fluctuate from point to point.

The extreme heat and pressure at he center of the Earth would render this moot.

The object placed at the center of the Earth would also have to be a perfect sphere for this to work.

[moot]

[clerick]

Originally posted by shamroc
Serious question - has anyone ever sent anything down there ?

I mean, how can we really know for sure what's down there until we actually send something down there....

Assuming we sent down a highly resilient web cam at the end of a proverbial very long stick... would we be greeted with zero gravity, or the maniacal  smiling face of the dark lord himself ?

Shamroc

Nothing has ever come close to the center of the earth and i doubt we ever will.  The tremendous heat and pressure would destroy anything barring some ultra-futuristic device.  

To help illustrate:

A skydiver falling at terminal velocity would take approximately 32 hours to fall to the center of the earth (ignoring the change in gravity he would experience on the way down).

The deepest hole drilled (as far as i could Google) was about 15 kilometers, that means we have only penetrated .002% of the Earth's crust.

[APDrone]

Originally posted by rogwar
VALE Inco
Creighton Nickel Mine

Sudbury, Ontario

Interesting!  So was it warm down there?  How's the air pressure?  Do you have to contend with air composition issues, like.. too much oxygen ( as opposed to the 'thin air' at Mile-high?)  

Never done any research on deep air depths ( probably know more about deep sea stuff ).

And the real important question.. what would the equivalent be to the mile-high club?

[Chairboy]

Batfink, with respect, you're mistaken, and your "anyone who disagrees with me is wrong because they're disagreeing with me" stance is kinda weak.

Clerick's post is spot on (and of course he's right about the uneven distribution of mass) and his diagrams should help you understand what's happening.

There's nothing magical about the center of the mass that makes it the place exerting the pull.  It's the mass itself that exerts the pull, not the very center.  So if you were at the center of an undifferentiated mass, you'd be pulled in all directions by the mass around you.

[RTHolmes]

hmmm chairboy and clerick both wrong here im afraid. if you are at the centre of our (hollow) earth you are not being pulled/pushed outwards towards the mass around you, you are being pulled/pushed towards the centre of mass of the entire object.

easy proof - move 1 foot from the CoM and you will return to it. If you were being pulled by the mass around you, you would keep on going out until you hit the "roof" of the inner chamber.

the pull/push thing is just linguistics, as bat alluded to.

and back OT rogwar thats a great trip  - how did it feel? noticeably warmer down there? get bends on the way back up?

[Chairboy]

Maybe it's semantics at this point, RTHolmes, because if you're at the center of mass and then you move to one side, there's more mass pulling at you on one side so you float back to the center.  But when you're at the center, you're being pulled equally in all directions.

Compare this with Batfink's assertion that some force is "pushing down on you".

[clerick]

Originally posted by RTHolmes
easy proof - move 1 foot from the CoM and you will return to it. If you were being pulled by the mass around you, you would keep on going out until you hit the "roof" of the inner chamber.

I'd like to see an empirical test that proves your first point.  According to my thinking, and i am still mulling this one over, i would have to believe that your second assertion is correct and you would indeed wind up on the "roof."  Since the gravity increases/decreases with distance, moving closer to one part of the "chamber" would increase the force pulling you to that side of the chamber and decrease the force exerted by the opposite side.  Now, this is assuming that there is no actual mass at he CoM but a hollow chamber, if it were a solid object then i do believe that you would return to the CoM.

the pull/push thing is just linguistics, as bat alluded to.

Gravity is an attractive force, NOT a repelling force.  It is not like electrical charges or magnetism, it will NOT push!  Its important to keep the terms correct for clarity.

[Chairboy]

I sketched this up quickly, pardon the crudeness:

In figure A, the object is at the exact center of mass.  The arrows indicate that the force being exerted on it is towards mass.  Every atom in the universe attracts every other atom, it's just big lumps of it that make a noticeable force.  

When the spherical object is in the center like in figure A, it would essentially be 'weightless' because it's being pulled equally in all directions.

If you move it to one side, like in figure b, then there's less mass on the left side exerting force and more mass on the right side, which would tend to pull it back towards the center, at which point it would appear weightless again. It's not, actually, it is experiencing something like G/pi^3 (my math might be wrong, no coffee yet), but it's from all directions, so in practice, it appears weightless.

[AKIron]

Originally posted by Chairboy
Batfink, ask yourself what causes gravity.

If you can come up with the answer to this you will become famous. A real answer that is, not that it is an intrinsic quality of mass. Or, something equally undefinitive like it's the bending of space by mass. You will need to answer why and how mass bends space.



In one of my less lucid moments I imagined that space is full of holes with the pressure of time forcing mass through them creating the illusion of gravity. I know, I should switch from scotch to beer.

[SkyRock]

Originally posted by Jebus


I know there is Hot Lava down there, but what if there wasnt?

Yes you would float, but just in a sea of molten nickel!:aok