Thoughts on the Current Flight Model

[MiloMorai]

Early P-38s also had trouble with regulating the turbocharger, as did the B-17 and B-24s.

For some reason they also had troubles caused by using Brit avgas.

[Tac]

Well how about this for the list:

1- 38 flaps auto-retracting

2- 38 guns able to fire 1 .50 cal gun at a time if you 'tap' the trigger (all 4 should fire at the same time)

[Stoney74]

Originally posted by MiloMorai
Early P-38s also had trouble with regulating the turbocharger, as did the B-17 and B-24s.

Somehow 8th Air Force was able to manage 1,000 aircraft missions of 17's and 24's that were escorted by a couple of groups of P-38's regardless.  I know this thread turned into a P-38 boost thread, but I honestly don't see how any of this bears on the game, since the dang turbo works every single time you turn the engine on, regardless of altitude.  It could be fathomable that if HTC raised the boost levels on the U.S. rides, the Spits, and even the 109K4 to the levels listed above, they'd have to perk the whole damn lot of them.  I'm content with my currently modelled Jug manifold pressure the way it is, and I've been spanked by enough P-38's and K4's in their current configurations to know that they are plenty effective as they are currently represented.  If they kicked the MP up to 70 inches, and as a result had to put a light perk on the plane, it would kill it for me.  Just leave it be and don't demand uber performance in your favorite ride from what I would consider, IMHO a planeset that is currently balanced, relatively speaking, to what it was in real life.  It may not be 100% accurate, but its probably close to a 90% solution.  And, given the plethora of variables, contradictory historical documentation, and all the residual historic sludge that exists on the Web, I'd say 90% may be as close as they can get, with respect to the different aircraft.  Bugs are one thing, but arguing over 10" of manifold pressure that was only available to one Air Force out of 15 that existed in WWII I believe is pointless.  If they want to add it to CT in an 8th AF setting, that's their perogative, and will certainly be their decision.  Meanwhile, in the rest of the war, this conversation has no bearing.  If the flight model could be tweaked to better represent stall characteristics, torque, p-factor, and all those other things we initially started talking about, that's another matter.

My last post on this subject.  Widewing, I look forward to your next thread regarding this--at least the first dozen posts or so.

[Knegel]

Yep Stoney, absolutly right!!!

At the end the relations matter not the static datas, like Vmax etc and as you say, the relations in AH looks rather good to me and i love to fly the 190A8 and P47īs!!

Greetings,

Knegel

[Widewing]

Originally posted by mw
Pierre Clostermann (Free French) wrote of the Tempest:
    It had a thoroughbred look and, in spite of the big radiator which gave it an angry and wilful appearance, it was astonishingly slender. It was very heavy, all of seven tons. Thanks to its 2,400 h.p. engine it had a considerable margin of excess power and its acceleration was phenomenal.

I routinely find myself questioning Clostermann's statements. Like Brown, I think he has a tendency towards overstating. However, in this case I think he's not far off.

First, let me use an  image from one of your documents. It is not data in the sense that it defines acceleration. It does, however, establish a general ranking in terms of relativity. So, is this accurate? We will see.



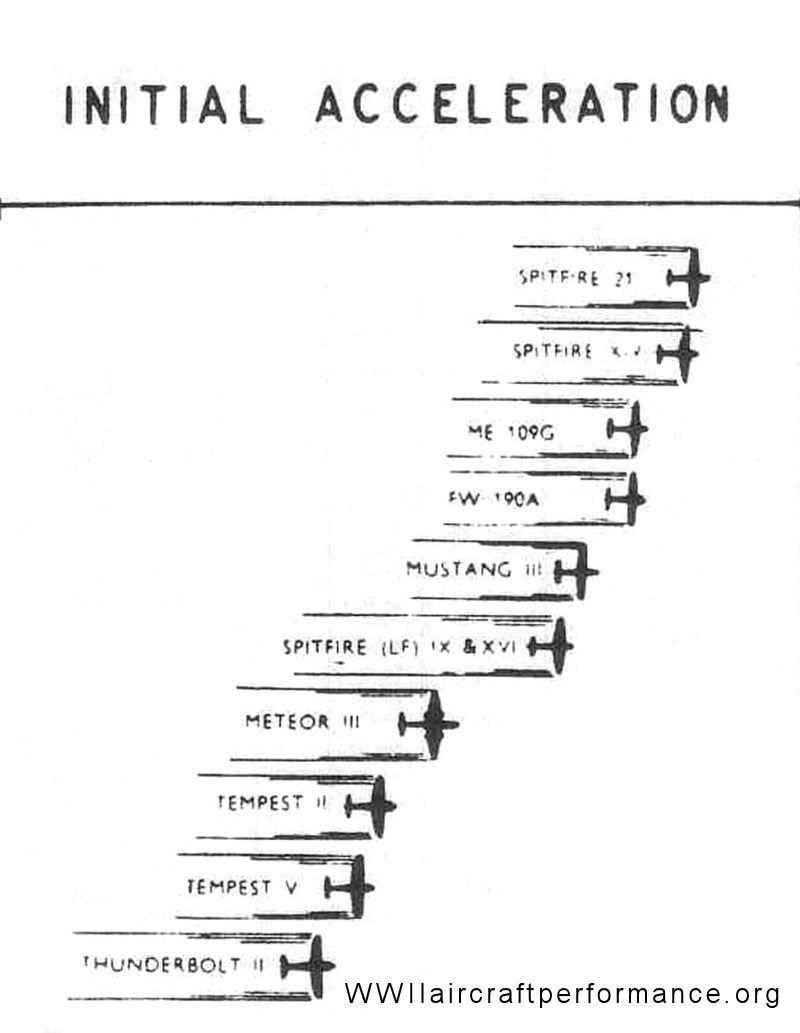
We can calculate a reasonably close rate of acceleration if we can determine several unknowns. These are propeller efficency and drag. We can use a constant for the the prop, but may have to estimate drag.

We can calculate the approximate thrust available at a given speed. To do this, we must estimate the efficiency of the propeller. If we begin at 150 mph, a typical WWII prop will demonstrate approximately 70% efficiency. If this is applied to all examples, it becomes a fair, if not perfectly accurate method. Note that 2,400 hp in the Tempest is at 11 lb boost.

Thus, for the Tempest:

375 x .7 x 2,400 / 150 = 4,200 lb of thrust.

For the Spitfire Mk.XIV:

375 x .7 x 2050 / 150 = 3,588 lb of thrust.

Now that we know the available thrust, we can calculate acceleration in feet per second, per second. Of course, we need to know what the total drag is. This can also be calculated or obtained from a reliable source. In this case, I'm going to use what I believe are close estimates.

Total drag for the Tempest: 1,350 lb

Total drag for the Spit XIV: 990 lb

Thus, thrust - drag / mass (in slugs) = initial acceleration in feet per second, per second.

Tempest: 4200 - 1350 / (11480/32.2) = 7.99 feet per second, per second.

Spit XIV: 3588 - 1090 / (8500/32.2) = 9.46 feet per second, per second.

Let's toss in the P-51D for comparison. I am calculating based upon an empty rear aux fuel tank (always burned off first on climb-out)

P-51D: 3010 - 845 / (9611/32.2) = 7.25 feet per second, per second.

Results, initial acceleration rate in g:

Spitfire Mk.XIV: 0.294 g
Tempest Mk.V: 0.248 g
P-51D: 0.225 g

Initial acceleration in the game, full load except for P-51D with 75% fuel. Time to accelerate from 150 mph to 200 mph at 100 feet ASL.

Spitfire Mk.XIV: 8.12 seconds (18 lb boost)
Tempest Mk.V: 8.16 seconds (10.5 lb boost)
P-51D: 10.81 seconds (67 in/hg boost)

The relationship between the Spitfire XIV and P-51D is reasonably close to the calculated acceleration (30% calculated vs 33% actual testing)

However, the difference between the Tempest and P-51D is much different (10% calculated vs 32% actual testing). In short, the AH2 Tempest appears to accelerate much faster than it should for the given boost and horsepower. Even if I reduce the Tempest's drag by 200 lb, it still should not accelerate as fast as it does in the game.

By the way, this tends to show that the acceleration chart above is flawed.

My regards,

Widewing

[Stoney74]

Originally posted by Widewing
By the way, this tends to show that the acceleration chart above is flawed.

My regards,

Widewing

Could it be that the chart is giving a representation of relative performance at typical combat altitude or would that even affect it?  By that, I mean would the comparison between a P-47 and Tempest at 25,000 feet be less or more closely represented by the chart than the same relation between sea-level acceleration?  I'm not sure about the Sabre in the Tempest, but at the P-47's critical altitude, some of the engines in the planes on this chart would be wheezing, relatively speaking, right?

[Widewing]

Originally posted by Stoney74
Could it be that the chart is giving a representation of relative performance at typical combat altitude or would that even affect it?  By that, I mean would the comparison between a P-47 and Tempest at 25,000 feet be less or more closely represented by the chart than the same relation between sea-level acceleration?  I'm not sure about the Sabre in the Tempest, but at the P-47's critical altitude, some of the engines in the planes on this chart would be wheezing, relatively speaking, right?

Though the document does not specify what altitudes were used, it does at least hint that the chart represents sea level acceleration.

Here's a quote from the related text:

"The ability to accelerate quickly is of paramount importance to fighters and the interceptor class has an obvious advantage in this respect. For comparative purposes it is impracticable to take into account maximum speed as acceleration is only operationally useful at the slower speeds when an interception suddenly has to be made from slow cruising.

For instance, the Tempest V, which is faster than the Spitfire XIV, takes less time to reach any given speed, but the Spitfire has the best acceleration, followed by the Mustang III, Tempest V, Thunderbolt and Meteor III. The unhappy position of the Meteor is accounted for by the natural sluggishness of early jets at the lower speeds. Here again, the power to weight ratio coupled with clean lines in design has considerable effect."

In one regard, there seems to be a contradiction. "For instance, the Tempest V, which is faster than the Spitfire XIV, takes less time to reach any given speed, but the Spitfire has the best acceleration,"

If the Spit XIV accelerates faster, it will reach a given speed faster. However, acceleration rates vary as your speed increases. In the game, from 150 mph to 200 mph, the Spitfire XIV accelerates faster and reaches 200 mph sooner. However, from 200 mph to 250 mph, the Tempest accelerates faster and thus, reaches 250 mph sooner. Perhaps, this is what the author meant.

My regards,

Widewing