Derivatives.
With: h small, (x + h)^(p/q) ≈ x^(p/q) [1 + (p/q)(h/x) + O(h/x)^2
Thus: limit h->0 [f(x + h) - f(x)]/h ≈ [x^(p/q) + (p/q)hx^(p/q - 1) +O(h/x)^2 - x^(p/q)] / h
≈ (p/q)x^((p/q)-1) +O(h)
Thus: if f(x) = x^(p/q), f ' (x) = (p/q) x^((p/q)-1)
Thanks for your input, but you've missed the point of the post.
The point has nothing, whatsoever, to do with calculus. In fact, gibberish might have been more effective.
Oh look at me... I too can post math formulas, do you like multi-dimensional DCTS, formulas currently being used for many video/audio compression algorithms such as H.264 (Actually H.264 uses a modified/simplified version that is more akin to 8 *8 spatial block transform).

or would you prefer
or would you prefer wavelet transforms used in JPEG2000 & Dirac Video compression algorithms which is applied to 4:2:2 color space (extra points if you know why?)
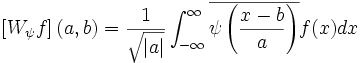
If you want, I can throw in some inverse Jacobian matrices and a practical application for LU decomposition (frequently used in IK computations)?
look at me, I also know math... and wikipeda to help math equations look better

sorry, this thread has gotten way off track, from mindless jokes around chest beating & tool shedding to straight up "I know more than you" first grade behavior.