Okay, this has given me an extreme curiousity...how does one get the lift and drag coefficients for things likes the fuselage alone of a WWII airplane?
Friday night with kids asleep -- so, I'll take a crack at it.

One could do it computationally, but it would require more work than I can put into it. One could do it in a wind tunnel, but that's out. Or, one can always do an estimation. That's within my grasp.
For a lifting body, L = 0.5 * rho * v^2 * S * C_L, where rho is air density, v is velocity of the aircraft, S is reference area for the object generating aerodynamic lift, and C_L is the coefficient of lift for that object. For wings, it is customary for S to be mean chord times wingspan. For knife edge, the fuselage is doing the aerodynamic lifting, and I'll take S to be 0.5 * (fuselage diameter at nose of aircraft) * (aircraft length) = 0.5 * d * l.
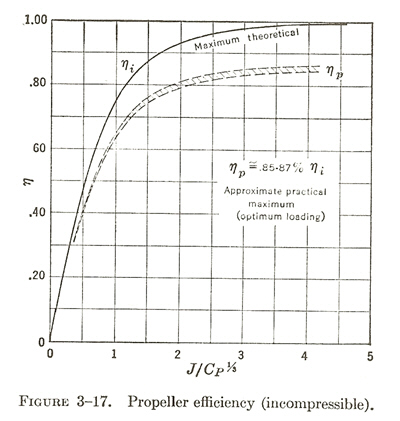
For thrust, from propeller theory (see
http://electraforge.com/brooke/flightsims/aces_high/stallSpeedMath/turningMath.html ), T= eta * BHP * 375 / v, where eta is propeller efficiency, BHP is HP of the engine. For props with good ability to absorb the power of the engine, eta can be approximated reasonably well by knowing the advance ratio (J) and the power coefficient (C_P): J = 88.0 * v / (N * D), where v is aircraft speed in mph, N is prop rotation in RPM, and D is prop diameter in feet; and C_P = 52.5 * gamma* BHP / [(N / 1000)^3 * D^5 * rho / rho_0], where gamma is fraction of full power being applied, BHP is engine brake horsepower, N is prop RPM, D is prop diameter in ft, rho is the air density, and rho_0 is the air density at standard sea level; and by using this chart:
I'm going to use a Pitts Special as a reference aircraft to see what a fuselage C_L is (as I can look at this video):
http://www.youtube.com/watch?v=xvn_PTs0e5Q And use these as references:
http://www.mt-propeller.com/pdf/stcflyer/FL003US.pdfhttps://en.wikipedia.org/wiki/Lycoming_O-540http://rgl.faa.gov/Regulatory_and_Guidance_Library/rgMakeModel.nsf/0/ffae5a2bb5506dcc8625747a00650001/$FILE/1E4.pdf
https://en.wikipedia.org/wiki/Pitts_Specialhttp://www.steenaero.com/Images/Aircraft/3Views/pitts_s1c_3-view_800x500.jpgMy Pitts estimates are:
v = 175 mph (approximate cruise speed for a Pitts Special)
HP = 300 HP
D = 7 ft
N = 2700 RPM
W = 1400 lbs
alpha = 30 degrees (just eyeballing it from video)
l = 19 ft
d = 95 / 516 * 19 = 3.5 ft
For this, J = 88 * 175 * / (2700 * 7) = 0.81. C_P = 52.5 * 300 / (2.7^3 * 7^5) = 0.048. J/C_P^(1/3) = 0.81/0.048^0.333 = 2.22. Then, eta = 0.8, and T = 0.8 * 300 * 375 / 175 = 514 lbs.
At sea level, rho = 1.22 kg/m^3 = mass/vol. The equivalent weight/vol in English units is 0.0762 lbs/ft^3 = mass * g / vol = rho * g, so rho = 0.0762 / 32.2 = 0.00237 lbs * s^2 / ft^4. For using in, say, L = 0.5 * rho * v^2 * S * C_L, where L is in lbs, v is in mph, and S in ft^2, we want rho in units of lbs / (mph^2 * ft^2), which is rho = 0.00237 lbs * s^2 / ft^4 * (5280 ft / mi)^2 * (1 hr / 3600 s)^2 = 0.00510 lbs / (mph^2 * ft^2).
L = W = 0.5 * rho * v^2 * S * C_L + T * sin(alpha). 1400 = 0.5 * 0.00510 * 175^2 * 0.5 * 19 * 3.5 * C_L + 514 * sin(30 deg). 1400 = 2600 * C_L + 257. C_L = 0.44.
OK, so my estimate is that a fuselage has a C_L of 0.44.
Now let's see what v we need on a Brewster to keep level in knife edge at the same 30 deg. For a Brewster, from America's Hundred Thousdand, by Dean:
HP = 1000 HP
D = 9 ft
N = 2200 RPM (had a gear ratio of 1:1)
W = 5500 lbs
l = 26 ft
d = 10 / 58 * 26 ft = 4.5 ft
So that I don't have to do a lot of algebra for a nonlinear equation, let's see if we can assume eta = 0.8 for the Brewster. Assume we'll need to be going at least 200 mph. In that case, J = 88 * 200 / (2200 * 9) = 0.89. C_P = 52.5 * 1000 / (2.2^3 * 9^5) = 0.084. J / C_P^(1/3) = 0.89 / 0.084^0.333 = 2.04, and eta = about 0.8 again. So, we are OK.
Then, T = 0.8 * 1000 * 375 / v. W = L = 5500 = 0.5 * 0.0051 * v^2 * 0.5 * 26 * 4.5 * 0.44 + 0.8 * 1000 * 375 / v * sin(30 deg). 5500 = 0.0656 * v^2 + 150,000 / v. 0.0656 * v^3 - 5500 * v + 150,000 = 0. Solving numerically for v gives a root at v = 275 mph.
So, with all of these estimates, it shows that a Brewster can maintain level, knife-edge flight at 275 mph or more.
This is all assuming that I haven't made any math errors. Also, if you think any of my numbers are wrong (like prop diameter of the Pitts Special, or whatever), plug in your own numbers and have a go at it.